
Inhoudsopgave:
- Auteur Sierra Becker becker@designhomebox.com.
- Public 2024-02-26 06:03.
- Laatst gewijzigd 2025-01-22 22:12.
Vaak, om een enkele beslissing te nemen, wordt er een munt opgeworpen, in de verwachting een vogel of een nummer te zien. In zeldzame gevallen zal de munt op zijn rand vallen, waardoor de "beslisser" wordt verward.

Weinig mensen denken dat het gebruik van een munt, een soort "ja/nee"-methode, zelfs in wiskundige experimenten wordt gebruikt, en specifiek in de kansrekening. Alleen in dit geval wordt het concept van een symmetrische munt soms een eerlijke of wiskundige munt gebruikt. Dit betekent dat de dichtheid over de hele munt hetzelfde is en dat kop of munt met dezelfde kans kan vallen. Naast de namen van de partijen die bekend zijn geworden, heeft zo'n munt geen tekens meer. Geen gewicht, geen kleur, geen maat. Zo'n munt kan slechts twee resultaten opleveren - omgekeerd of omgekeerd, er zijn geen "op de rand" in de kansrekening.
Alles in de wereld is waarschijnlijk
Kansrekening is een heel gebied dat nog steeds probeert het toeval te bedwingen en alle mogelijke uitkomsten van gebeurtenissen te berekenen. Dankzij formules en talrijke empirische methoden maakt deze wetenschap het mogelijk om te oordelenredelijke verwachting. Als we vertrouwen op de betekenis van wat werd gezegd door professor P. Laplace (hij leverde een belangrijke bijdrage aan de ontwikkeling van de theorie), dan is de essentie van alle acties in de waarschijnlijkheidstheorie een poging om de actie van gezond verstand te verminderen naar berekeningen.
Het woord "waarschijnlijk" verwijst rechtstreeks naar deze wetenschap. Het begrip "aanname" wordt gebruikt, wat betekent: het is mogelijk dat er een gebeurtenis zal plaatsvinden. Als we dichter bij wiskunde komen, dan is het meest opvallende voorbeeld het opgooien van een munt. En dan kunnen we aannemen: in een willekeurig experiment wordt een symmetrische munt 100 keer opgeworpen. Het is waarschijnlijk dat het embleem bovenaan staat - van 45 tot 55 keer. Pas dan begint de veronderstelling te worden bevestigd of bewezen door berekeningen.
Berekenen tegen intuïtie
Je kunt een tegenbewering doen en je wenden tot intuïtie. Maar wat te doen als de taak moeilijker wordt? In praktische experimenten kan meer dan één symmetrische munt worden gebruikt. En dan zijn er nog meer opties-combinaties: twee adelaars, staarten en een adelaar, twee staarten. De kans om uit elke optie te vallen wordt al anders, en de combinatie "omgekeerd - voorzijde" verdubbelt in uitval in vergelijking met twee adelaars of twee staarten. De natuurwetten zullen in ieder geval worden bevestigd door fysieke experimenten, en deze situatie kan op dezelfde manier worden geverifieerd door echte munten op te gooien.

Er zijn situaties waarin intuïtie nog moeilijker te weerstaan is aan wiskundige berekeningen. Het is onmogelijk om alle opties te voorspellen of te voelen als er nog meer munten zijn. Wiskundige hulpmiddelen worden in het bedrijf geïntroduceerd,gerelateerd aan combinatorische analyse.
Voorbeeld om te ontleden
In een willekeurig experiment wordt drie keer een symmetrische munt opgeworpen. Je moet de kans berekenen dat je bij alle drie de worpen staarten krijgt.
Berekeningen. Staarten moeten in 100% van de gevallen van het experiment (3 keer) uitvallen, dit is een van de 8 combinaties: drie koppen, twee koppen en staarten, enz. Dit betekent dat de kansberekening wordt gedaan door 100% te delen door het totaal aantal opties. Dat is 1/8. We krijgen het antwoord 0, 125.
Er zijn tal van problemen voor een symmetrische munt. Maar er zijn voorbeelden in de kanstheorie die zelfs mensen zullen interesseren die verre van wiskunde zijn.
Doornroosje
Een van de paradoxen die aan A. Elga worden toegeschreven, heeft een 'fantastische' naam. Dit vat heel goed de essentie van de paradox. Dit is een probleem dat verschillende antwoorden heeft, en elk van hen is correct op zijn eigen manier. Het voorbeeld laat duidelijk zien hoe gemakkelijk het is om op de resultaten te werken met het meest winstgevende resultaat.
Doornroosje (de heldin van het experiment) wordt verdoofd met slaappillen via een injectie. Hierbij wordt een symmetrische munt opgeworpen. Wanneer de kant met de adelaar eruit v alt, wordt de heldin gewekt en eindigt het experiment. Met een resultaat met staarten wordt de schoonheid gewekt, waarna ze weer in slaap worden gebracht om de volgende dag van het experiment wakker te worden. Tegelijkertijd vergeet de schoonheid dat ze wakker werd, hoewel ze de omstandigheden van het experiment kent, afgezien van de informatie op welke dag ze wakker werd. Vervolgens - de meest interessante vraag, specifiek voor de ontwaakte schoonheid: "Bereken de kans om een kant met staarten te krijgen."

Er zijn twee oplossingen voor dit paradoxale voorbeeld.
In het eerste geval zonder goede informatie over de wake-ups en de resultaten van de munten. Aangezien het om een symmetrische munt gaat, wordt precies 50% verkregen.
Tweede beslissing: voor exacte gegevens wordt het experiment 1000 keer uitgevoerd. Het blijkt dat de schoonheid 500 keer werd gewekt als er een adelaar was, en 1000 keer als het staarten waren. (Bij de uitslag met staarten werd de heldin immers twee keer gevraagd). Dienovereenkomstig is de kans 2/3.
Vital
Zulke manipulatie van gegevens in statistieken komt voor in het leven. Bijvoorbeeld informatie over het aandeel gepensioneerden in het openbaar vervoer. Volgens informatie wordt 40% van de reizen gemaakt door gepensioneerden. Maar in feite maken gepensioneerden geen 0,4 van de totale bevolking uit. Dit wordt verklaard door het feit dat gepensioneerden actiever gebruik maken van vervoersdiensten. In werkelijkheid wordt het aantal gepensioneerden geregistreerd binnen 18-20%. Als we alleen rekening houden met de meest recente passagiersreis en niet met de vorige, dan zal het percentage gepensioneerden in het totale passagiersvervoer rond de 20% liggen. Als u alle gegevens opslaat, dan alle 40%. Het hangt allemaal af van het onderwerp dat deze gegevens gebruikt. Marketeers hebben het eerste cijfer nodig van de werkelijke vertoningen van hun advertenties aan de doelgroep, transportmedewerkers zijn geïnteresseerd in het totale aantal.
Het is opmerkelijk dat er toch iets uit de wiskundige lay-outs in het echte leven lekte. Het was de symmetrische munt die begon te worden gebruikt om geschillen op te lossen vanwege het eerlijke karakter en de afwezigheid van tekenen van partijdigheid. Bijvoorbeeld sportscheidsrechtersze gooien het wanneer het nodig is om te bepalen welke van de deelnemers de eerste zet zal krijgen.
Aanbevolen:
Wat is sluitertijd? In welke gevallen wordt deze functie gebruikt en is deze nodig in de camera?

De camera is een apparaat met veel functies en mogelijkheden. Afhankelijk van de combinaties van deze parameters wordt zelfs bij het fotograferen van hetzelfde object een radicaal ander resultaat bereikt. Om te beginnen is het de moeite waard om te weten wat de sluitertijd is, wanneer deze nodig is en welk effect ermee bereikt kan worden
Waar wordt de Franse naad gebruikt? Zijn uitvoeringstechniek en een korte beschrijving van andere soorten naden

Waarschijnlijk heeft elk meisje op school bij handwerklessen de basissoorten naden geleerd voor naaien met de hand en machinaal. Maar na verloop van tijd verdwijnen deze vaardigheden. En als het nodig is om kennis in de praktijk toe te passen, wordt het een bijna onmogelijke opgave. U moet onmiddellijk onthouden hoe u een Franse naad moet maken, hoe u de stof moet instoppen en de kunst van het inrijgen van de onder- en bovendraad in de machine opnieuw moet leren. Alle textielverwerkingstechnologieën zijn onderverdeeld in twee groepen. Het is gemakkelijk om ze te onthouden
Wat is het verschil tussen een spiegelreflexcamera en een digitale camera en waarom wordt deze vraag verkeerd gesteld?
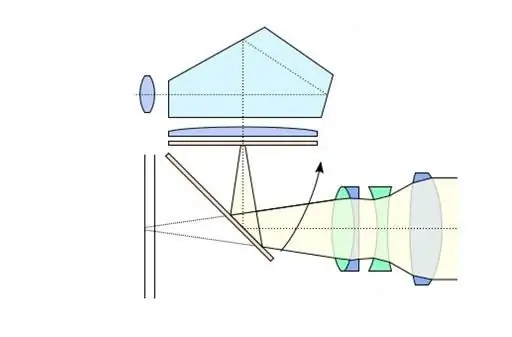
In het artikel zullen we praten over wat het karakteristieke kenmerk is van digitale en analoge spiegelreflexcamera's
Waar wordt konijnenpoot voor gebruikt? Kenmerken van het maken van een talisman

Zoals oude legendes zeggen, is de betekenis van talismannen altijd van groot belang geweest voor hun eigenaren. Aanvankelijk was de hoofdpersoon van veel overtuigingen een haas, maar na verloop van tijd verspreidden magische eigenschappen zich naar een konijn
Wat is transparant plastic en hoe wordt het gebruikt in de kunst?

Relatief recentelijk verscheen er een nieuw soort creativiteit in Rusland - modelleren van polymeerklei. Dit materiaal lijkt op plasticine, maar is handiger bij het werken met kleine details. Bovendien moet polymeerklei of plastic gebakken worden in een luchtgrill of oven. Dit is nodig om het product dat van dit materiaal is gemaakt aan kracht en flexibiliteit te laten winnen
